Formula For Stdev In Excel
Understanding Standard Deviation in Excel

Standard deviation is a measure of the amount of variation or dispersion of a set of values. In Excel, calculating the standard deviation can be done using several formulas, depending on the type of standard deviation you want to calculate. The two main types are population standard deviation and sample standard deviation.
Population Standard Deviation

The population standard deviation is used when you have data for the entire population. The formula for population standard deviation in Excel is STDEV.P. This function calculates the standard deviation of a population based on the entire population of data.
To calculate the population standard deviation, you can use the formula: =STDEV.P(number1, [number2],…)
Where: - number1 is required and represents the first number in the population. - [number2],… are optional and represent additional numbers in the population.
For example, if you have a set of numbers in cells A1 through A10, you can calculate the population standard deviation using the formula: =STDEV.P(A1:A10)
Sample Standard Deviation

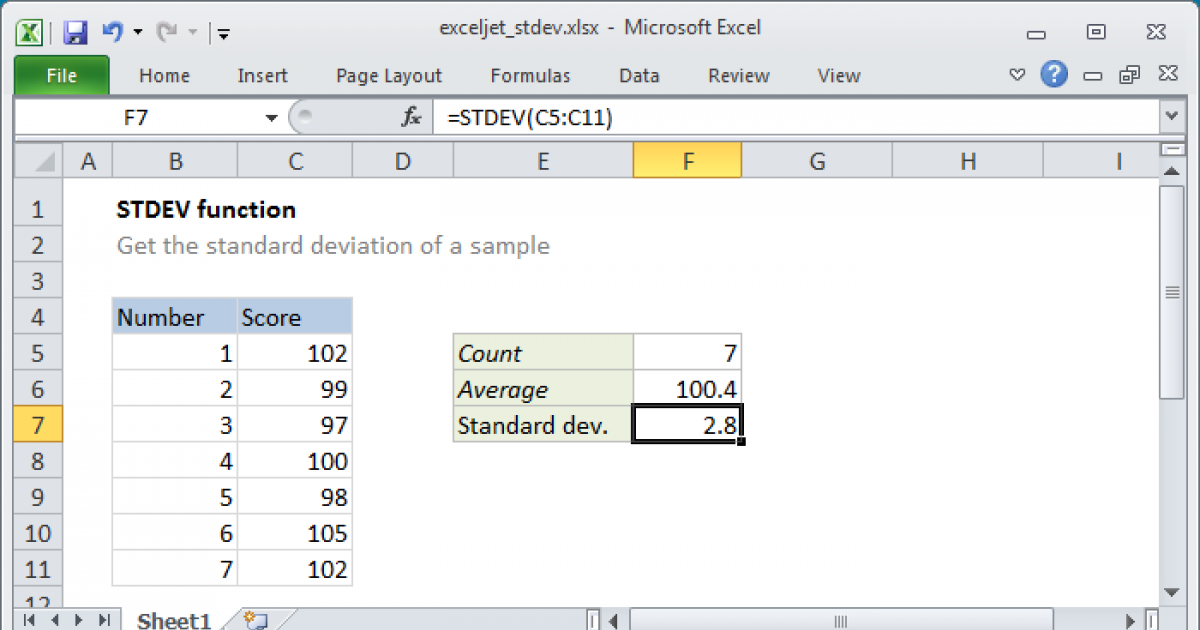
The sample standard deviation is used when you have data for a sample of the population. The formula for sample standard deviation in Excel is STDEV.S. This function calculates the standard deviation of a sample based on a sample of data.
To calculate the sample standard deviation, you can use the formula: =STDEV.S(number1, [number2],…)
Where: - number1 is required and represents the first number in the sample. - [number2],… are optional and represent additional numbers in the sample.
For example, if you have a set of numbers in cells A1 through A10, you can calculate the sample standard deviation using the formula: =STDEV.S(A1:A10)
Older Versions of Excel

In older versions of Excel (before Excel 2013), the functions STDEV and STDEVP were used instead of STDEV.S and STDEV.P.
- STDEV was used to calculate the sample standard deviation.
- STDEVP was used to calculate the population standard deviation.
To calculate the sample standard deviation in older versions, you can use the formula: =STDEV(number1, [number2],…)
To calculate the population standard deviation in older versions, you can use the formula: =STDEVP(number1, [number2],…)
📝 Note: When working with standard deviation, it's crucial to understand whether your data represents a population or a sample to choose the correct formula.
Practical Applications

Standard deviation has many practical applications in finance, engineering, and other fields. For instance, in finance, standard deviation is used to measure the volatility of a stock or portfolio. A higher standard deviation indicates a higher level of risk.
Calculating Standard Deviation Manually

Although Excel provides built-in functions to calculate standard deviation, understanding how to calculate it manually can be beneficial. The manual calculation involves finding the mean of the dataset, then subtracting the mean from each value to find the deviation, squaring each deviation, summing these squared deviations, dividing by the number of items (for population standard deviation) or the number of items minus one (for sample standard deviation), and finally taking the square root of this result.
The formula for manual calculation of population standard deviation is: [ \sigma = \sqrt{\frac{\sum(x_i - \mu)^2}{N}} ]
The formula for manual calculation of sample standard deviation is: [ s = \sqrt{\frac{\sum(x_i - \bar{x})^2}{n-1}} ]
Where: - (x_i) represents each individual data point, - (\mu) is the mean of the population, - (\bar{x}) is the mean of the sample, - (N) is the number of items in the population, - (n) is the number of items in the sample.
Visual Representation

Embedding images or charts can help illustrate the concept of standard deviation and how it affects data distribution. For instance, a bell curve (normal distribution) with a small standard deviation will be taller and narrower, indicating that most data points are close to the mean. Conversely, a bell curve with a large standard deviation will be shorter and wider, indicating that data points are more spread out.
| Standard Deviation Type | Excel Formula | Description |
|---|---|---|
| Population Standard Deviation | =STDEV.P(number1, [number2],...) | Calculates the standard deviation of a population. |
| Sample Standard Deviation | =STDEV.S(number1, [number2],...) | Calculates the standard deviation of a sample. |

In summary, calculating standard deviation in Excel is straightforward using the STDEV.P and STDEV.S functions for population and sample standard deviations, respectively. Understanding the difference between these two types of standard deviations and knowing how to apply them is crucial for accurate data analysis.
What is the main difference between STDEV.P and STDEV.S in Excel?

+
The main difference is that STDEV.P is used for calculating the population standard deviation, while STDEV.S is used for the sample standard deviation. The former divides by the number of items (N), and the latter divides by the number of items minus one (n-1).
How do I decide whether to use population or sample standard deviation?

+
You should use the population standard deviation if you have data for the entire population. If your data represents a sample of the population, you should use the sample standard deviation.
Can I calculate standard deviation manually without using Excel functions?

+
Yes, you can calculate standard deviation manually by finding the mean, subtracting the mean from each value, squaring each result, summing these, dividing by the appropriate number (N for population, n-1 for sample), and taking the square root of this result.